Resume en français

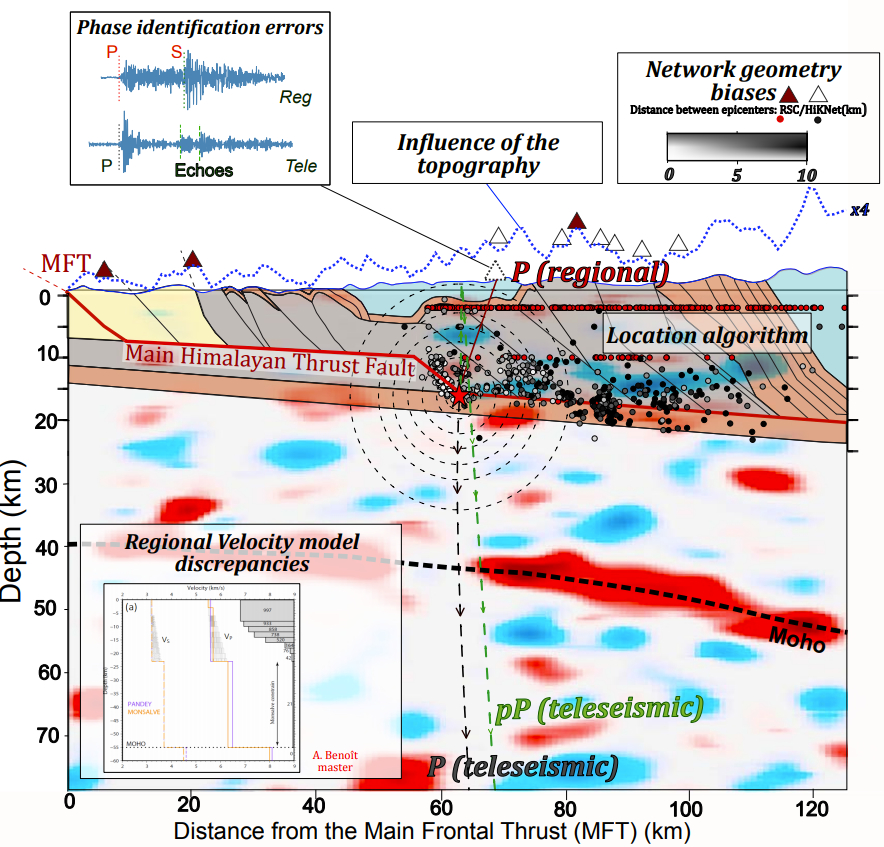
Les localisations hypocentrales des séismes sont généralement obtenues par des méthodes d’inversion des arrivées des phases P et S observées aux différentes stations d’un réseau sismologique fixé. La quantification des incertitudes de localisation, notamment pour l’estimation de la profondeur, doit être améliorée pour une meilleure fiabilité des interprétations sismotectoniques et, surtout, de l’évaluation de l’aléa sismique. Dans cet article, nous proposons de mettre en lumière les effets des principales sources d’incertitude dans le problème de localisation à travers une analyse de sensibilité globale. Les analyses de sensibilité permettent de quantifier les effets de différentes variables d’entrée sur la variance de la sortie d’un problème. Dans cette étude, nous prenons en compte trois facteurs principaux : la géométrie du réseau de stations, la présence d’erreurs dans les observations des temps d’arrivées des phases P et S, et les erreurs dans les hypothèses d’un modèle de vitesse 1D, afin d’observer leurs effets individuels et combinés sur la localisation d’un séisme. Ces multiples sources d’incertitudes sont décrites par une douzaine de variables aléatoires dans notre modèle. Nous utilisons une approche d’échantillonnage de Monte-Carlo pour explorer les différentes configurations du modèle dans un schéma itératif. Les différences entre la localisation initiale “de référence” de la source sismique et les 100 000 localisations hypocentrales résultantes, obtenues par l’exploration des différentes configurations, sont analysées et interprétées à l’aide de la méthode de décomposition de la variance introduite par Sobol (1993). Cette approche, appliquée pour la première fois en sismologie, nous offre une première quantification de l’importance relative de nos variables d’entrée sur les différents paramètres de localisation, comprenant la localisation épicentrale, la profondeur et le temps origine de l’évènement. Entre autres choses, elle met en évidence l’importance critique de l’approximation du modèle de vitesse et fournit un nouvel aperçu objectif et quantitatif pour comprendre les sources d’incertitudes dans le processus d’inversion.

English abstract

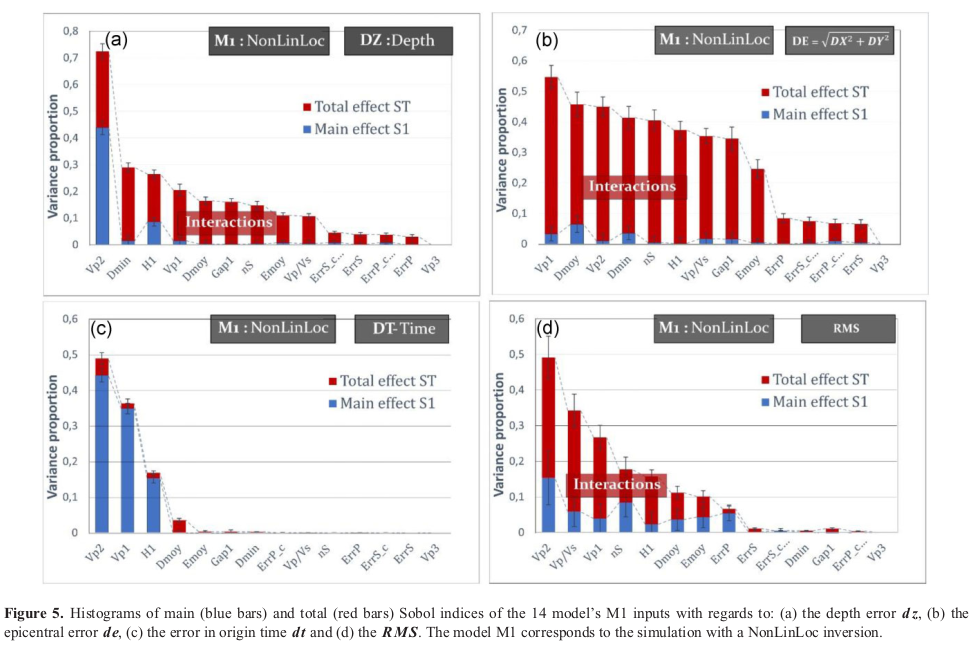
The hypocentral locations of earthquakes are generally obtained by inversion methods of the P and S phase arrivals observed at the various stations of a fixed seismological network. The quantification of localization uncertainties, particularly for depth estimation, needs to be improved to enhance the reliability of seismotectonic interpretations and, above all, seismic hazard assessment. In this paper, we propose to highlight the effects of the main sources of uncertainty in the localization problem through a global sensitivity analysis.Sensitivity analyses are used to quantify the effects of different input variables on the variance of a problem’s output. In this study, we consider three main factors: the geometry of the station network, the presence of errors in the observations of P and S phase arrival times, and errors in the assumptions of a 1D velocity model, in order to observe their individual and combined effects on earthquake localization. These multiple sources of uncertainty are described by a dozen random variables in our model.We use a Monte-Carlo sampling approach to explore the different model configurations in an iterative scheme. The differences between the initial “reference” location of the seismic source and the resulting 100,000 hypocentral locations, obtained by exploring the different configurations, are analyzed and interpreted using the variance decomposition method introduced by Sobol (1993). This approach, applied for the first time in seismology, provides us with an initial quantification of the relative importance of our input variables on the various location parameters, including epicentral location, depth and time of origin of the event. Among other things, it highlights the critical importance of the velocity model approximation and provides a new objective and quantitative insight into the sources of uncertainty in the inversion process.

• Download the paper here